Как рассчитать доходность? Метод Арсагеры
- 77
- 74728

В данном материале рассказывается о том, как правильно рассчитать доходность портфеля ценных бумаг с учетом вводов/выводов (движения денежных средств).
Как рассчитать доходность? На первый взгляд, дать ответ на этот вопрос несложно. Многие знают, что для того чтобы посчитать доходность, необходимо результат инвестиций разделить на сумму вложенных средств и перевести полученное значение в годовые проценты.
Формула расчета доходности (в % годовых), если не происходило вводов/выводов:
D = ((ΔS)/Sнач) * 365/T * 100%, где
- D – искомая доходность;
- ΔS – результат инвестирования в абсолюте;
- Sнач – сумма первоначальных инвестиций;
- T – количество дней в рассматриваемом периоде.
Но задача расчета доходности многократно усложняется в случае, если в течение рассматриваемого периода осуществлялись вводы и/или выводы средств в рамках инвестиционного портфеля. В таком виде она вызывает затруднения даже у опытных специалистов в области инвестиций. Кроме того, не существует идеального способа подсчета доходности в этом случае, поэтому необходимо согласиться (и хорошо их понимать) с определенными допущениями, которые используются в том или ином методе. Мы предлагаем свое решение данной задачи. Сравнение нашего метода с другими известными способами подсчета доходности будет приведено в отдельном материале.
Начнем с определения того, что же такое вводы и выводы денежных средств. Ввод денежных средств – это направление денег на инвестиции. К примеру, Вы приобрели инвестиционные паи фонда или внесли деньги на брокерский счет – все это является вводом средств. Изъятие инвестиционных средств является выводом средств, то есть в рамках наших примеров выводы возникают при погашении инвестиционных паев или выводе денег с брокерского счета.
Зная, что же такое вводы/выводы, рассмотрим конкретную ситуацию, которая поможет понять логику решения задачи по корректному определению доходности с учетом вводов/выводов средств.
- Некий инвестор приобрел акций на сумму в 1 000 ₽ (Sнач).
- Через 3 месяца он купил еще акций на 500 ₽ (Sвв).
- Еще через 4 месяца инвестору срочно понадобились деньги, и он был вынужден продать часть акций на сумму в 300 ₽ (Sвыв).
- Через год после первоначального приобретения стоимость акций составила 1 300 ₽ (Sитог).
В виде графика данную ситуацию можно представить следующим образом:
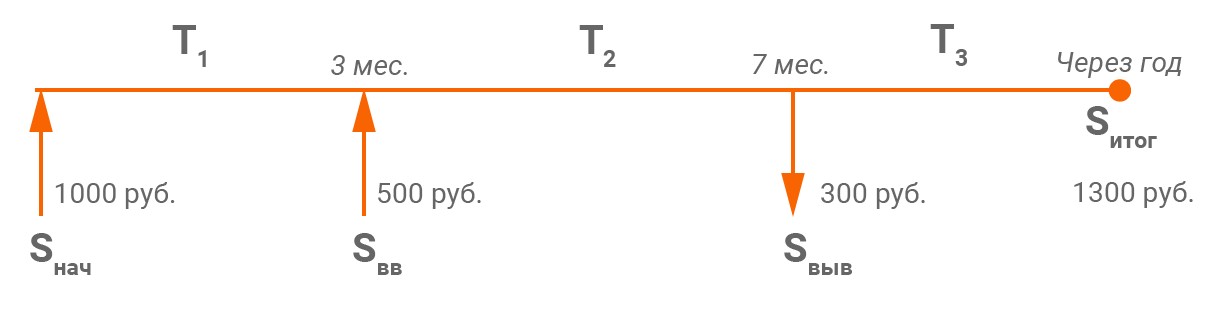
Чтобы корректно рассчитать доходность от инвестиций, нам по-прежнему необходимо разделить результат инвестиций на сумму вложенных средств. Остается только определить, что в рассматриваемой ситуации является результатом и какова корректная сумма вложенных средств.
Первым шагом будет расчет результата инвестиций. И в этом отношении нет никакой сложности, кроме того, финансовый результат вычисляется абсолютно точно. Результат инвестиций – это разница между тем, что мы вывели и имеем на конец периода, и тем, что было вложено. То есть необходимо из суммы стоимости инвестиций на конец периода и всех выводов за период вычесть сумму начального и всех последующих вводов.
Формула для определения результата инвестирования с учетом вводов/выводов:
ΔS = (Sитог + ΣSвыв) – (Sнач + ΣSвв), где
- ΔS – результат инвестирования за период в абсолюте;
- Sитог – итоговая оценка инвестиций (1 300);
- ΣSвыв – сумма всех выводов средств (300);
- Sнач – сумма первоначальных инвестиций (1 000);
- ΣSвв – сумма всех вводов средств (500).
Применим данную формулу к рассмотренной ситуации: ΔS = (1 300 + 300) – (1 000 + 500) = 100. Таким образом, инвестор заработал 100 ₽.
Есть любители считать сумму вложенных средств без учета денег, которые были введены на счет (брокерский), но на которые не приобретались ценные бумаги. Такой расчет может резко завысить доходность, хотя прибыль по инвестициям от этого не увеличится. Этот расчет неверен, денежная составляющая инвестиционного портфеля при расчете суммы вложенных средств должна учитываться в полном объеме. Неверно рассчитывать доходность только на часть портфеля, ведь средства, введенные на счет, отвлечены от других целей (потребления, накопления и др.) и являются инвестициями, доходность которых и необходимо узнать.
Второй шаг в расчете доходности является наиболее важным: необходимо корректно определить, с какой суммой соотносить рассчитанный результат инвестирования. А еще точнее, вычислить размер средств в виде единой суммы, которой инвестор как бы оперировал в течение всего периода.
Необходимо согласиться со следующей логикой: в каждый временной подпериод сумма, которой оперировал инвестор, была разной. Начальная сумма была «рабочей» до первого момента ввода или вывода, затем, чтобы понять «рабочую» сумму на следующем подпериоде, её нужно скорректировать на размер ввода (увеличить) или вывода (уменьшить), и так далее для каждого подпериода до конца срока, за который считается доходность.
В подпериод T1: 1 000 ₽, T2: (1 000 + 500) ₽, T3: (1 000 + 500 – 300) ₽. Кроме того, сами по себе эти временные подпериоды не равны. T1 = 90 дней, T2 = 120 дней, T3 = 155 дней. Поэтому необходимо взвесить соответствующую «рабочую» сумму на количество дней в подпериоде, определив таким образом единую средневзвешенную по времени «рабочую» сумму на всем рассматриваемом периоде.
Формула для определения средневзвешенной суммы с учетом вводов/выводов:
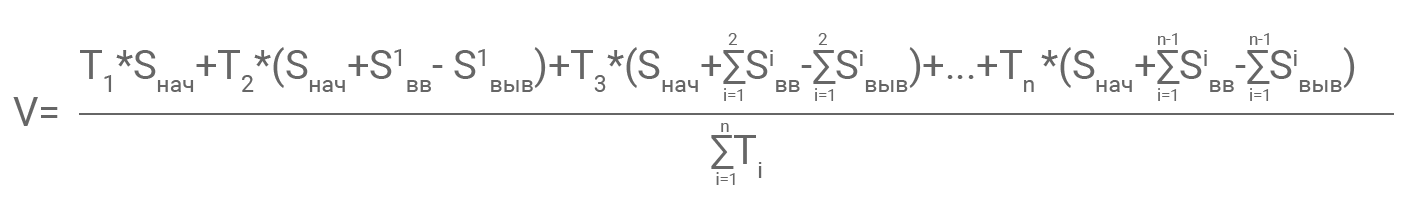
где V – средневзвешенная сумма,
T1, T2, T3, ..., Tn – количество дней в подпериоде,
ΣTi – суммарное количество дней на рассматриваемом временном отрезке.
Применим данную формулу к рассмотренной ситуации:
V = (90 * 1 000 + 120 * (1 000 + 500) + 155 * (1 000 + 500 – 300))/365 = 1 249,32.
Средневзвешенная сумма вложенных инвестором средств составила 1 249,32 ₽.
Теперь известны все элементы, необходимые для непосредственного расчета доходности.
Если Вы хотите рассчитать доходность на периоде, который не включает в себя первоначальный ввод средств, то за Sнач необходимо принять стоимость инвестиционного портфеля на ту дату, с которой Вы хотите начать расчет доходности.
Третий шаг – расчет доходности из полученных значений. Для этого поделим рассчитанный ранее результат инвестирования на средневзвешенную сумму вложенных средств и переведем полученный результат в годовые проценты.
Формула следующая: D = (ΔS/V) * 365/T * 100%
Получается, что в рассмотренной ситуации доходность составляет: (100/1 249,32) * 365/365 * 100% = 8% годовых.
Это аналогично тому, что у инвестора не было никаких вводов/выводов, и он просто в самом начале вложил сумму в размере 1 249,32 ₽, весь период ей оперировал, а в итоге получил прибыль в размере 100 ₽.
Также можно использовать формулу, учитывающую сложный процент:
D = (1 + (ΔS/V))365/T – 1
Используя данные формулы, Вы всегда сможете корректно оценить доходность инвестиционного портфеля и при помощи полученных значений оценить эффективность Ваших инвестиций.
Теперь рассмотрим некоторые нестандартные случаи, с которыми можно столкнуться на практике (у нас они случались не раз).
1-й вырожденный случай
Рассмотрим следующий пример:
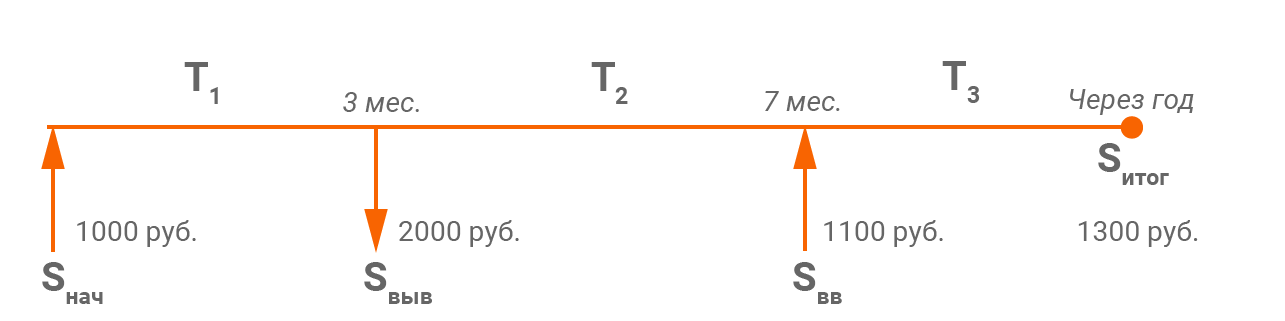
Ввели 1 000 ₽, спустя 3 месяца наши инвестиции утроились (вот такая удача!), что позволило нам вывести 2000 ₽, затем через 7 месяцев мы ввели сумму 1100 ₽, а по окончании года с момента начала инвестиций стоимость нашего портфеля составила 1300 ₽. Таким образом, прибыль за весь срок:
ΔS = (1 300 + 2 000) – (1 000 + 1 100) = 1 200
С оценкой прибыли проблем никаких нет – здесь все корректно, как и произошло на практике.
А вот с расчетом средневзвешенной рабочей суммы возникают сложности. На втором временном отрезке сумма получается отрицательная (– 1 000). Вес ее настолько велик, что и вся средневзвешенная сумма на периоде получается отрицательной.
V = (90 * 1 000 + 120 * (1 000 – 2 000) + 155 * (1 000 – 2 000 + 1 100))/365 = (90 * 1 000 + 120 * (-1 000) + 155 * 100)/365 = –39,73
Корректно оценить размер полученной доходности не получается. Поэтому мы доработали наш метод. В таких случаях, отрицательные суммы, получившиеся на определенных временных отрезках, делаем равными нулю (считаем, что работа ведется заработанной ранее прибылью, то есть нулевой рабочей суммой на этом подпериоде). Как следствие, если:

Таким образом, в данном примере:
V = (90 * 1 000 + 120 * (1 000 – 2 000) + 155 * (1 000 – 2 000 + 1 100))/365 = (90 * 1 000 + 120 * 0 + 155 * 100)/365 = 289,04
Далее
D = (ΔS/V) * 365/T * 100% = (1 200/289,04) * 365/365 * 100% = 415,17% годовых.
Или D = (1 + (ΔS/V))365/T – 1 = (1+(1 200/289,04))365/365 – 1 = 4,1517 или 415,17% годовых.
Данный результат, на наш взгляд, является значительно более правдоподобным.
2-й вырожденный случай
Предположим, Вы осуществляете регулярные инвестиции и в начале каждого квартала в течение 2 лет вносите определенную сумму, например, 1 000 ₽. Таким образом вы внесли 8 000 ₽ за весь период. Несложно посчитать, что средневзвешенная рабочая сумма на этом периоде составит 4 500 ₽.
Например, на рынке случился грандиозный обвал (так было в конце 2008 года), и стоимость Вашего портфеля на конец периода составила 3 000 ₽. Рассчитаем доходность таких инвестиций:
ΔS = 3 000 – 8 000 = – 5 000
Таким образом, отрицательная переоценка больше половины внесенных средств и, что особенно важно, превышает размер средневзвешенной рабочей суммы 5 000 > 4 500. Тогда расчет по формуле:
D = (1 + (ΔS/V))365/T – 1, становится не возможен!
D = (1 + (–5 000/4 500))365/730 – 1, так как отсутствует математическая возможность вычисления квадратного корня из отрицательного числа.
Действительно, ситуация выглядит несколько абсурдно, так как потери как бы превышают рабочую сумму. При этом, естественно, потери не больше суммы всех внесенных средств.
В таких случаях мы используем исключительно простую формулу доходности:
D = (ΔS/V) * 365/T * 100% = (–5 000/4 500) * 365/730 * 100% = –55,56% годовых.
Она, пусть и при определенных допущениях, но более наглядно оценивает доходность таких инвестиций.
Выводы
- Необходимо очень внимательно относиться к расчету доходности, так как этот показатель является определяющим для оценки эффективности инвестирования.
- Не существует идеального способа вычисления доходности портфеля, если происходили вводы/выводы. Необходимо согласиться с некоторыми допущениями.
- Рассмотренный алгоритм не является простым, но, на наш взгляд, это самый точный и универсальный метод подсчета доходности. Данный алгоритм позволяет учесть все нюансы, связанные с вводами/выводами средств, и получить корректный расчет доходности.
- Правильно оценивайте результат в некоторых вырожденных случаях, с которыми может столкнуться любой инвестор.
- Если Вы пользуетесь услугами доверительного управления, узнайте, каким образом происходит расчет прибыли и доходности по Вашему портфелю, и если он отличается от обозначенного выше алгоритма, то это повод проверить корректность применяемого алгоритма.